Archive List for そろばん通信

そろばんと算数・数学の関係？ 　中学生の保護者と話しているとき、お母さんが、ふと、 「うちの子は、数学が嫌いなんです。本人がいうには、お母さんが、無理やりソロバンを習わせたから、数学が嫌いになったんだって、主張します。わたしは、本人のためを考えて、ソロバンを習わせたのですが・・・」 　と愚痴をこぼしました。 「そろばんを習ったから、算数・数学が嫌いになるなんてことは、ありません。数学嫌いの言い訳として、そろばんを口実にしているだけです。でも、ひとつ、問題なのは、〔無理やり〕という部分ですね。そろばんに限らず、無理強いされると、ほとんどの場合、子どもはそのことが嫌いになります。学習でも、スポーツでも、習い事でも、いやいややっていると、その取り組みに対して、いやなイメージが定着してしまいます。子どもに練習を無理強いするタイプのコーチにスポーツを習うと、そのスポーツが上手にならないだけでなく、そのスポーツを嫌いになってしまいます。たぶん、お子さまは、厳しいだけの先生に習って、いやな気分のままソロバンを練習していたのかもしれませんね」 　わたしがそう話しますと、お母さんは、思い当たることがあるようでした。 　なんどもいっていることですが、学習や練習の前に、かならずリラックスした状態をつくることが必要です。 　ところが、スパルタ型の先生は、子どもたちを緊張させた状態で、学習や練習に取り組ませることが多い。すると、脳の偏桃体という部位がいやな感情を増幅させて、データを処理する海馬という部位の働きを止めてしまいます。つまり、ブレーキをかけながら、学習したり、練習したりすることになります。 　とうぜん、楽しいはずがありませんね。 　みなさんは、楽しく、そろばんに取り組んでいますか？　楽しく取り組めているかぎり、そろばんで培った計算力は、算数・数学に対する強力な味方になります。 　さて、そろばんと算数・数学の関係ですが、筆算による計算は、脳にとって言語的な処理になります。ですから、筆算は、女性の脳のほうが強いでしょう。いっぽう、そろばんによる計算は、イメージ的な処理になりますから、男性の脳のほうが強いかもしれません。 　以前は、言語処理は左脳、イメージ処理は右脳、といわれていましたが、どちらの処理にも左脳・右脳ともに関わっていますので、左脳・右脳の機能は、あくまで脳の傾向です。ひとによっては、左右の働きが逆の場合もあります。 　女性の脳に弱点があるとすれば、空間認識能力がやや未熟であることでしょう。これは狩猟時代の先祖たちからの影響で、女性が自然空間のなかを狩りで飛び回らなかったことが遠い原因のようです。でも、男女に関わりなく、小学生の脳は柔軟ですから、傾向として苦手なことも訓練によって克服できます。たとえば、同時通訳など、言語の変換は女性の脳のほうが優位ですが、女性に負けない男性の通訳者もたくさんいます。重要なことは、生まれつきの差ではなく、学習や練習なのです。 　そろばんの練習は、言語操作である計算をイメージ（そろばんの盤面は、数字ではないので、イメージ）で行いますから、空間認識をする部位（右脳の前方）をしっかりと使います。そろばんによって左脳と右脳の両方が鍛えられるわけですね。 　みなさんは、せっかく脳を鍛えたのですから、算数の問題にもしっかりと取り組みましょう。算数が嫌いな子どもの多くは計算が苦手ですが、みなさんは計算に強いのですから、算数の問題にたくさん取り組めるはずです。もし図形の問題が苦手だとしたら、まだ、二次元空間、三次元空間に慣れていないだけですから、たくさん問題を解けば、どんどんできるようになります。 　そろばんで培った力を算数や数学の世界に活かしましょう！ 山手学院　学院長　筒井保明

そろばんは練習だ！ 　そろばん学習の基本は「練習」です。そろばんは、「勉強」ではありません。 　「勉強」ということばは、もともと漢語（中国の昔の言葉）で、『礼記』や『中庸』という書籍に出てきます。みなさんにわかりやすくいえば、「勉強」は「しぶしぶやる」「いやいややる」「無理してやる」といった感じです。ですから、「勉強しろ」といわれると、みなさんも、いやな気持ちになるでしょう？ 　ちなみに関西の問屋街などで、「勉強してや」というと、「安くして」という意味になります。いまでは年配の人しか使わないようですが、「勉強してほしいなあ」といわれた問屋の主人は、そろばんの玉を弾いて、「これで、どないや」とそろばんの盤面を客に見せます。望みの金額になっていると、客は笑顔になって、交渉が成立します。「おおきに（ありがとう）」です。でも、値切られた主人の心のなかは、「しぶしぶ」「いやいや」「無理して」でしょう。だから、「勉強」というわけですね。 　いっぽう、「学習」ということばも漢語で、『礼記』に出てきます。わたしたちには、中学校で学ぶ『論語』の冒頭「学びて、ときにこれを習う。また、悦ばしからずや」でお馴染みのことばです。孔子は「学習って、たのしくて、うれしいものだよね」といっています。ですから、わたしは、「勉強」ということばを使わず、「学習」ということばを使います。 　ともあれ、そろばんは、けっして「勉強」ではないことをわかってください。 　そもそも「しぶしぶ」「いやいや」「無理して」そろばんを練習しても、思うように上達しません。学校の学習であっても、スポーツや習い事であっても、「しぶしぶ」「いやいや」「無理して」やっても、なかなかうまくなりません。 　なぜなら、みなさんが「しぶしぶ」「いやいや」「無理して」やっているとき、みなさんの脳は、感情をつかさどる偏桃体という部分が優位になっていて、学習をつかさどる海馬という部分にブレーキがかかっています。つまり、「しぶしぶ」「いやいや」「無理して」は、ブレーキをかけながら、自転車をこぐようなものです。当然、前に進みません！ 　これが、「勉強」が非効率で、「学習」が有効な理由です。 　さて、そろばんの学習の秘訣は、「少しずつ何回も」です。そろばんの計算方法を理解したら、あとは練習を重ねます。練習すればするほど、そろばんの計算は、正確で速くなります。 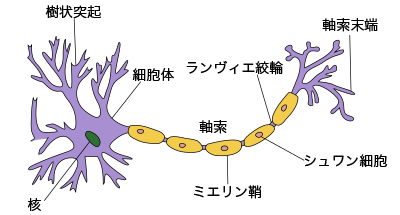　そろばんの計算方法を理解した段階では、脳の神経細胞が情報伝達経路としてシナプス結合した状態です。このとき、神経細胞の軸索にまだ髄鞘（ミエリン鞘）はできていません。おなじ刺激をくりかえしますと、髄鞘化され、情報の伝達速度が加速されます。 　そろばんも、学習も、スポーツも、芸術も、はじめのころは、意識的に取り組むしかありませんので、ゆっくりと時間がかかります。ところが、おなじ刺激をくりかえしているうちに、おなじ動作なら、どんどんと速くなります。これが練習の成果です。 　もし、みなさんが、自分のそろばんの速度に満足していないなら、まだまだ練習が足りないだけです。正確で速いそろばんは、練習によって実現できます。 　そういっても、最初は、ていねいに基本を学ぶこと！　まちがえて学んでしまうと、練習しても成果が上がりません。「学びて、ときにこれを習う」です。 　たのしく学んで、「少しずつ何回も」そろばんを練習しましょう。 山手学院　学院長　筒井保明

そろばんでどこまで計算できるの？ 　みなさんのおじいさん・おばあさんの子どものころは、そろばんという道具は、現在より、もっと身近なものでした。算盤には大きなものから小さなものまで、また長いものから短いものまで、本当にさまざまな種類のものがあって、わたしの家にも、商売をしていたせいか、碁石ほどの大きさの玉をつらねた木製のそろばんから、手のひらサイズの華奢な小さなそろばん、また、一、十、百、千、万、億、兆、京、垓、秭（𥝱）、穣、溝、澗まで計算できる長さのものまで、さまざまなそろばんがありました。ただし、わたしの場合、そろばんとして用いられることは少なくて、たいてい、現在のブレードボードや、むかし流行ったローラースケートのようなものになっていました。 　ところで、漢数字の桁をアラビア数字で表しますと、下記のようになります。 一 1 十 10 百 100 千 1,000 万 10,000 億（万万） 100,000,000 兆（万億） 1,000,000,000,000 京（万兆） 10,000,000,000,000,000 垓（万京） 100,000,000,000,000,000,000 　一般的な23桁そろばん、少し長い27桁そろばんのどちらでもまだ計算できますね。 　垓のつぎの秭（𥝱）になりますと、万垓ですから、1,000,000,000,000,000,000,000,000となり、23桁そろばんではもう計算できません。 　わたしの手元にある明治時代に出版された『算盤の独稽古』篠田正作著（算盤を一人で練習するための手引き書）には、覚えるべき暗記数目として、〔基数〕一、二、三、四、五、六、七、八、九、〔大数〕一、十、百、千、万、億、兆、京、垓、秭（𥝱）、穣、溝、澗、〔小数〕分、釐、毫、絲、忽、微、繊、沙、塵、埃、渺、漠　を上げています。使わない単位を覚えよとはいわないでしょうから、きっと使う機会があったのだと思います。 　ちなみに、当時、江戸時代からの習慣で、奇数は、半目の数、偶数は丁目の数といいます。さいころを二つ振って、偶数か奇数かを争う「丁か半か」はここから来ています。 　ともあれ、よほどの関心がないかぎり、むかしの手引き書を読む必要はありません。なぜなら、『算盤の独稽古』に書かれていることの多くはもう必要でないからです。 　たとえば、着物を作るのに使う布のことを反物（端物）といいますが、「一反は二丈六尺のものあり、または二丈七尺、二丈八尺等種々あり」とあいまいに書かれています。丈は十尺、尺は十寸。寸は、中学生になると、『竹取物語』で約3.03cmと覚えることになります。かぐや姫の身長が3寸ばかりで、約９㎝。ですから、二丈七尺は約８ｍ18cmだと計算できますが、現在ではあまり役に立ちませんね。（でも、古文をはじめとして、十進法によるメートル法が採用される以前の書籍を読むためには必要です） 　みなさんもとても長い算盤を目にする機会があるでしょう。長いのは、大きな数を計算できるようにするためです。25桁の秭（𥝱）の先には、穣、溝、澗、正、載、極、恒河沙、阿僧祇、那由他、不可思議、無量大数と続きます。そろばんの長さをどんどん長くしていけば、時間はものすごくかかるでしょうが、数字がそこにあるかぎり、そろばんの計算は可能なのです。 山手学院　学院長　筒井保明

そろばんは小学生にふさわしい! 　お年寄りの回想録を読んでいたとき、 「不思議なことに、何十年もそろばんを手に取っていなかったのに、小学生のときに身につけたそろばんや暗算は、いまもやろうと思えば、できるのですよ」 　というセリフがありました。 　たしかに、そろばん検定を取得している大人たちに聞いても、 「ずいぶん長いあいだ、やっていませんが、いまでも自然にできますね。暗算は日常で使っていますから当然かもしれませんが、そろばんもだいじょうぶです」 　というような返答が大半です。 　ときどき、 「もう忘れちゃったかな。でも、ちょっと練習すれば、いけるかな」 　という弱気な発言もありますが、「ちょっと練習すれば」というところにすこし自信が見えますね。 　そろばんだけでなく、小学生のときにしっかりと身につけた能力は、大人になっても失われることはないようです。水泳やバスケットボールのようなスポーツでも、ピアノやバイオリンのような音楽でも、小学生のうちに身につけたことは、大人になってもできるのです。 　いっぽう、大人になってから、小学生とおなじ学習をしようとすると、そろばんでも、スポーツでも、芸術でも、大人はなかなか上達しないのです。途中であきらめてしまう大人のほうが多いかもしれません。なにごとでも身につけるためには単純な反復練習が必要なのですが、小学生には耐えられても、多くの大人たちは耐えられないからです。 　単純な繰り返し練習が必要な習い事やスポーツは、小学生のうちにやっておくのが正解でしょう。 　なかなか新しいことが身につかない大人たちを見て、クリティカルエイジやクリティカルピリオド（学習の臨界期）のような仮説が立てられたのではないでしょうか。学習の臨界期というのは、ある年齢を超えると、新しい学習が身につけられないのではないか、という考えです。たとえば、音声認識（絶対音感など）であれば５歳くらいまで、言語能力であれば８～13歳くらいまで、という仮説です。 　全体の傾向として、大人たちを見ていますと、クリティカルエイジやクリティカルピリオドが存在するような気がしますが、もちろん例外的な大人たちもいますから、やはり仮説ですね。 　そういっても、そろばんに関していえば、はじめてそろばんを習う小学生と大人では、小学生のほうがまちがいなく上達が速いでしょう。 　お年寄りの回想のとおり、小学生のときに身につけた能力は、ずっと長持ちします。 　そろばんの練習は、小学生にふさわしい学習です。 山手学院　学院長　筒井保明

競技としてのそろばん 　毎年、8月8日「そろばんの日」に全国珠算教育連盟主催の全日本珠算選手権大会が開催されます。そろばん日本一を決定する個人総合競技をはじめとして、各種目別競技に全国の選手たちがチャレンジします。 　柔道や剣道や空手などの武道から、さまざまなスポーツ、また、ゲームや暗記や早食いにも競技がありますから、競技としてのそろばんにもまったく違和感はないでしょう。むしろ、そろばんは計算速度の世界でもありますから、F１やインディカーのレースのように、熟達者は、自然と、そろばんの正確さと速度を競いたくなるではないでしょうか。だからこそ、おなじように、ゲームにも、暗記にも、早食いや大食いにも、競技が成立するのです。 　NHK大河ドラマ「青天を衝け」の主人公、藍商人の息子であった渋沢栄一もそろばんの熟達者でしたから、きっと誰よりも速く計算できることに快感を覚えていたはずです。じつは、ゆっくりとそろばんを操作するよりも、できるだけ速くそろばんを操作するほうが、気持ちもいいし、計算にもまちがいが少ないのです。あわてることはだめですが、どんなに速くても、そろばんの操作が快活であれば、計算は正確になります。 　わたしは、残念ながら、「青天を衝け」を見ていないのですが、毎週、欠かさずに見ている教師から、「藍の買い付けなどでは、当然、算盤が出てきましたが、一橋家の重要な場面でも算盤が出てきましたよ」という報告を受けています。 　慶喜に対して、「武士とて、金は入り用。それがしは一橋家の懐具合を整えたいのです」といって、算盤をバンと取り出し、「ふところを豊かにし、その土台を頑丈にする。軍事よりはむしろ、そのような御用こそ、おのれの長所でございます」と断言した場面のようです。 　江戸時代は、その末期といえども、儒学が国教として生きていました。中国の思想家である孔子（紀元前552年―紀元前479年）の教えを編集した『論語』がその中心です。 　「孔子は、理財（経済）を説いていないのではないか」という疑問に対して、渋沢栄一は、断固として否定し、「孔子が理財（経済）を理解していたことはまちがいない」と主張しています。だからこそ、「算盤は論語によってできている」と明言できたのです。 　上記の慶喜との対面の場面に登場したそろばんは、もちろん論語によってできているそろばんでしょう。徳川家康の再来といわれた徳川慶喜が『論語』を熟知していないはずがありません。論語算盤説を信念とする渋沢栄一は少年時代から「片手に論語、片手に算盤」です。渋沢の言葉は、慶喜の胸にも強く響いたはずです。 　平和な時代であれば、競技としてのそろばんを渋沢栄一は支持したであろうし、むしろ「渋沢栄一杯」などの大会を主催したかもしれません。なにしろ「国民が算盤を忘れたら、国が滅亡してしまう」という言葉を残しているくらいです。渋沢にとって、儒学（論語）と同等に、算盤は重要なものでした。「片手に論語、片手に算盤」で、はじめてバランスがとれるのです。 　大河ドラマが大評判になったあかつきには、「渋沢栄一杯」というような、そろばんの競技大会が開かれるかもしれませんね。 山手学院　学院長　筒井保明

渋沢栄一にとっての算盤 　NHKの大河ドラマ「青天を衝け」の主人公は、埼玉県深谷市生まれの渋沢栄一です。ドラマではあまり前面に出てこないかもしれませんが、渋沢栄一といえば、片手に『論語』を持ち、もう片手に「算盤」を持っているというのが、生前の代表的なイメージです。 　渋沢栄一は、さまざまな文章のなかで「算盤」という言葉を使っています。彼は「算盤」という言葉に「経済」「理財」「商売」「利殖」「金儲け」など、多くの意味を持たせています。どの言葉にもいつも具体的な算盤のイメージがついていますから、わたしは、「渋沢栄一は、ほんとうに算盤が好きだったんだなあ」と感じて、ほほ笑んでしまいます。 　渋沢の著書をたくさん読んでも、算盤の練習の話は出てきません。彼の実家は、武州榛澤群血洗島村（現深谷市）で、藍染め用の藍の製造を営んでいました。彼は14歳で商売の道に入り、掛け売り先に代金の回収にいったり、近隣の村々に藍染めの原料を買い入れにいったりするようになりました。このときには、もう算盤がしっかりと身についていたはずです。 　70歳の祝いのとき、友人から来た賀状に、論語と算盤とシルクハットと朱鞘の刀剣が描かれていました。どれも渋沢栄一の人生を象徴する書物や道具です。この絵を見ても、彼にとっての算盤の重要さがわかるでしょう。 　渋沢栄一は、道具としての算盤をまちがいなく使いこなしていました。珠算式暗算をやっていたかどうかはわからないのですが、その経歴を見るかぎり、抜群に計算に強かったはずです。算盤を基礎として、「商売」「経済」の世界に人生を広げていったのです。 　渋沢栄一は、重要なことを語るとき、「経済」とか「理財」という言葉ではなく、ずばり「算盤」といいます。 　たとえば、「もし国民が算盤を忘れ、儒学の理屈ばかりにとらわれ、虚栄に赴いてしまったら、国の元気を失い、国の生産力を弱め、最悪の場合、国が滅亡してしまう」といい、「算盤は論語によってできている。論語はまた算盤によって本当の活動されるものである。（この部分は原文のまま）だから、論語と算盤はとても遠いけれど、とても近いものであるといつも論じているのだ」と主張しています。 　生徒のみなさんは、まだ論語を読んだことがないでしょう。みなさんとおなじくらいの年のとき、渋沢栄一少年は、論語を暗記しています。このとき、藍を商っていた父親から、そろばんを習い覚えたのではないか、とわたしは想像しています。 　それにしても、「算盤は論語によってできている」という言葉はすごいですね。渋沢栄一は、算盤を使う仕事において、彼が立ち上げた会社や銀行において、けっして道義を外れたことはしませんでした。 　経済と道徳のバランスをとりながら、92年の生涯を生き抜いたといっていいでしょう。 　渋沢栄一少年は、おどろくべき読書家でした。しかし、読書だけでは、後年の渋沢栄一にならなかったでしょう。彼を「近代日本の資本主義の親」にしたのは、少年時代の「算盤」です。 　渋沢栄一の伝記などを読んでから、「算盤」を見直してみると、みなさんも自分の算盤に愛情が湧くのではないでしょうか。 山手学院　学院長　筒井保明

レオナルド・ダ・ヴィンチと珠算式暗算 　レオナルド・ダ・ヴィンチの天才の秘密に触れてみたかったら、ダ・ヴィンチとおなじトレーニングをしてみよう。 　まず、バラをしっかりと見る。花びら、がく、とげ、葉軸、小葉とできるだけ細部までしっかりと見る。そして、そのイメージを頭に焼き付ける。できたかな？ 　つぎに目を閉じて、いま見たバラの花を細部まで頭の中に再現してみるのだ。もちろん、リアルであれば、リアルなほどよい。 　やってみるとわかるのだが、思ったより頭が疲れるはずだ。リアルに思い浮かべようとすればするほど、息が切れるくらい、脳がエネルギーを使うからである。脳のエネルギー源はグルコース（ブドウ糖）と酸素だけれど、感覚としては酸素をものすごく使う。 　そもそも脳は、ひとの一日分のエネルギーの20％ほどを使う。もちろん、酸素の消費量がもっとも多いのも脳で、酸素の消費量も全体の25％ほどになる。ふつうに脳を使っていても、それだけ使うのだから、リアルにイメージを思い浮かべようとするトレーニングは、かなりきついものなのだ。でも、なんどもチャレンジしていると、だんだんリアルにイメージできるようになる。このイメージ再現能力がダ・ヴィンチの天才の秘密の一つなのだ。 　ダ・ヴィンチは、まちがいなくイメージで思考した。だから、ものすごい量のエネルギーをダ・ヴィンチの脳は消費した。こんなトレーニングを日常で行っていたのだから、ダ・ヴィンチの脳は、桁違いに優秀だったわけだ。 　この練習をしてみると、むしろ言葉は脳の手抜きではないかと思われるくらい、楽である。山や川のイメージを思い浮かべてみろ、といわれると、けっこうたいへんだが、「山」や「川」という言葉で置き換えてしまえば、ほとんどの人がほっとするだろう。 　珠算式暗算は、脳に思い浮かべた算盤のイメージを操作することだから、脳はかなりのエネルギーを使う。実際に算盤を使って計算するほうが楽で、珠算式暗算は、本人が思っているよりもはるかにエネルギーを使うはずだ。もし算盤を使用しているときと、珠算式暗算を行っているときの酸素の消費量を量ることができれば、きっとおもしろい結果になるだろう。 　みなさんは、ぜひ珠算式暗算で、脳のイメージ操作力を鍛えてください。イメージを操作することは、みなさんが予想しているよりもはるかに疲れるけれど、そのぶん、みなさんの脳は鍛えられる。 　「イメージが先。言葉が後」 　イメージを覚えたり、操作したりすることにはたくさんのエネルギーを使うけれど、いちど、その経験をしておくと、「言葉って、なんて楽で便利なものだろう」ということがわかる。 　もしレオナルド・ダ・ヴィンチの眼の前に算盤があったら、イメージ・トレーニングを使って、彼はあっというまに珠算式暗算の名人になったのではなかろうか。なぜなら、脳のなかでさまざまな花のイメージを細部まで再現できたダ・ヴィンチは、算盤をリアルに思い浮かべて操作することぐらい、かんたんにやってのけたであろうからだ。 山手学院　学院長　筒井保明

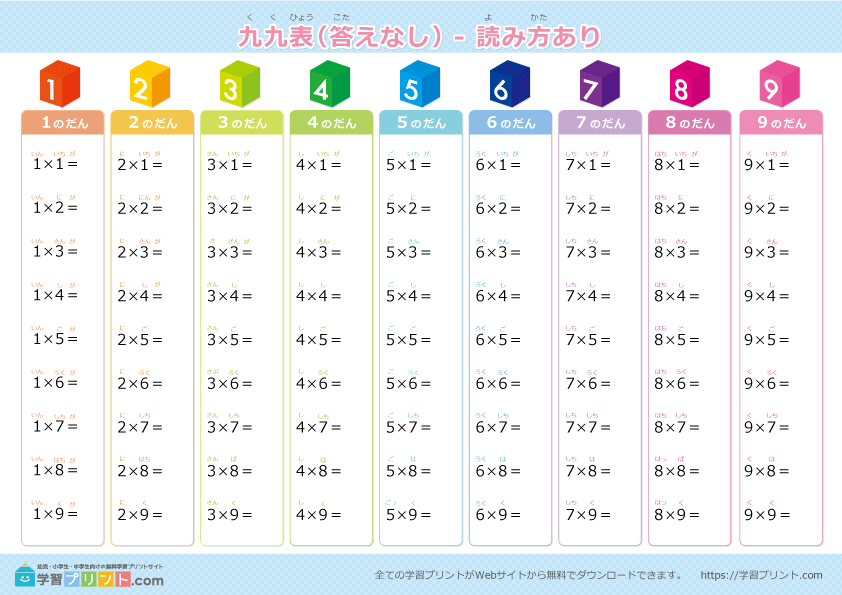
そろばんは体感だ！ 　数学史で九九の歴史をさかのぼりますと、半九九、また逆九九の記録が先に登場します。 　わたしたちがおぼえる総九九が日本で採用されたのは1925年ですから、それほどむかしではありません。 　九九は、基本的に暗記します。イメージを操作することもできますが、一般的には、数字という言語を使用した暗記といっていいでしょう。 　前回、３×３＝９（さざんがく）、４×２＝８（しにがはち）のように、「が」が残ったのは、そろばん教師のおかげであったことを話しました。当時の文部省は、（さんさんく）とか（しにはち）のように、「が」を捨てる指示を教師にしていたのです。 　せっかくそろばん教師たちが、唱えやすいように「が」を残したのですから、みなさんは声に出して九九を暗記しましょう。 　ところで、最近、総九九を逆にひっくりかえした逆九九表を学習プリント.comが無料で提供しています。 　９×９＝８１（くくはちじゅういち）から始まりますので、逆九九表です。この表を答えられるようにすると、柔軟に九九を使えるようになるでしょう。 　ただし、歴史的には、逆九九は、九九八十一から始めて、大きい数×小さい数、同じ数×同じ数、以外は省くのが本当です。 　さて、九九は、数字という言語を使用した暗記ですが、そろばんと決定的にちがうことがわかりますか？ 　そろばんの盤面は、約束によって、数字として読むことができますが、そろばんの玉一つ一つは、樺玉、柘植玉、黒檀玉、紫檀玉、梅玉など、どんな種類の玉であっても、そろばんの玉にすぎません。 　いっぽう、電卓は数字キーに数字が記入されていますから、数字という言語の操作です。 　そう考えてみますと、そろばんって、なんだか不思議な道具ですね。 　わたしが小学生のころにもどってみますと、そろばんの重みや手触り、また、玉を弾くときの感触や音感がよみがえってきます。電卓とは、ぜんぜんちがう世界が広がります。 　珠算式暗算でも、意識のどこかに、そろばんを弾いて練習したときの体感が残っているでしょう。 　そろばん以外でも、書道、絵画、彫刻、裁縫、弓道、剣道、料理など、道具を使う作業をくりかえしていますと、言葉ではうまく表現できない体感が身についてきます。 　小学生にとって、体感をともなう学習はとても重要です。 山手学院　学院長　筒井保明

ややこしい九九のはなし 　むかし（といっても大正・昭和のはじめ）のそろばんの本を読んでいると、半九九、順九九、逆九九、総九九というようなことが書いてあります。 　もっとむかし（江戸時代・明治時代）のそろばんの本を読むと、掛け算の九九だけでなく、割り算の九九まで出てきます。 　松下村塾の吉田松陰先生は、江戸時代の人ですから、門下生に割り算の九九まで教えていましたが、あんまりややこしいので、わたしは、最後まで読まないで投げ出してしまいました。 　左の図は、半九九の表で、文字どおり、九九が半分しかありません。同じ数×同じ数、小さい数×大きい数、以外の掛け算は省いてしまいます。順九九ともいいます。 　逆九九というのは、この表をひっくり返して、九九八十一から始めるのですが、同じ数×同じ数、大きい数×小さい数、以外の掛け算は省いてしまいます。 　これは、中国や日本のいちばん古い九九の記録が、半九九、逆九九のように書かれているからです。記述するのが、めんどうだっただけかもしれないのですが、伝統的に、中国や日本では、半九九、逆九九、でした。 　半九九と逆九九を足すと、総九九になります。 　現在では、ほとんどの九九の表は、総九九になっていますね。 　日本の学校教育で総九九が採用されたのは、大正14年（1925年）ですので、96年前のことです。当時は、先生自体が半九九（順九九）しかできませんでしたから、苦手な先生は総九九を教えることにずいぶん抵抗があったようです。 　そのうえ、たとえば、三五十五（3×5＝15）のうち、どちらが「かけられる数」で、どちらが「かける数」か、で議論がわかれていました。3の5倍は15、と考えるか、3倍の5は15、と考えるか、ということです。九九も意外とややこしいものです。 　ところで、当時の教師用の解説書には、九九の呼び声として、「二一二」「二二四」と呼べ、と書かれていました。 　これに対して、そろばんの教師たちが、「にいちに、ににし」では覚えにくい。そろばんで覚えるように、二一ガ二、二二ンガ四と唱えるほうが記憶しやすい」と反対しました。 　また、「ガ」が十の位にあたるので、そろばんの珠の置きまちがえがなくなると主張しました。 　たとえば、 　三一ガ三　3×1「ガ三」（03） 　三二ガ六　3×2「ガ六」（06） 　三三ガ九　3×3「ガ九」（09） 　三四十二　3×4「十二」（12） 　三五十五　3×5「十五」（15） 　九九の答えが二桁になるとき、「ガ」が入らないことに気がつきましたか？ 　九九の呼び声に「ガ」が残ったのは、そろばんの功績の一つでしょう。 　なにしろ、当時の文部省は、「ガ」を捨てようとしていたのですから。 　みなさんは、まず総九九をしっかりと自分のものにしてください。 山手学院　学院長　筒井保明

そろばん名人のひみつ 　３＋３を６と答えるとき、「３＋３」に対して、反射的に「６」という言葉を答えることを暗記的算数といいます。暗記的算数に関して、わたしは、九九などを除いて否定的な意見をもっていますが、計算能力として、 １＋１は、２ ２＋２は、４ ３＋３は、６ と反射的に覚えさせる教授法があることは事実です。暗記的算数のまま、小学生の算数をずっと先まで教えてしまう教室もあります。 　でも、これでいいのでしょうか？ 　暗記的算数は、どこまでいっても言葉の操作です。言葉の操作ですから、自由自在に広がることができません。 　物理学者のアインシュタインは、「数学でも物理でもイメージを操作した」と自分でいっています。重要なのは、言語の操作ではなく、イメージの操作です。 　上の計算をイメージに置き換えますと、 ●＋●は、●● ●●＋●●は、●●●● ●●●＋●●●は、●●●●●● になります。 　わたしは、イメージの操作こそ、小学生が学ぶべき方法だと考えています。 　そろばんは、そろばん上のイメージの操作です。数学史的にいっても、小学生にふさわしい学習です。 　ひとの思考のおおもとはイメージです。ずいぶん以前、「ひとは言葉で思考する。言葉がなければ思考できない」といわれていましたが、現在では「ひとはイメージで思考して、言葉で表現する」といわれます。 　たとえば、朝、コーヒーを入れようと考えます。お湯をわかし、コーヒー豆をひき、カップを用意し、ドリッパーをカップの上に置き、紙フィルターを開いてドリッパーに置き、ひいたコーヒーの粉を入れ、お湯を少し注ぎ、ちょっと蒸らしてから、さらにお湯を徐々に注ぎます。 　この行動に対して、最初は意識して言語化するかもしれませんが、なんどもコーヒーを入れて慣れてきますと、もう言語化することはありません。だまって、コーヒーを入れます。 　このコーヒーを入れるという行動を行わせているのは、イメージによる思考です。 　もしできあがったコーヒーの味がまずければ、コーヒー豆のひき具合を変えるとか、お湯の入れ方を変えるとか、言葉ではなく、イメージで思考します。コーヒーを上手に入れるためには、実践が必要なのであって、言葉ではありません。 　じつは、そろばん名人のひみつもおなじです。 　そろばんを習い始めのころは、意識して言葉にあらわすかもしれませんが、慣れてきたらイメージで計算して、最後の答えだけを言葉にあらわします。計算の途中段階をいちいち言葉になおしていたら、速い計算はできません。究極のそろばん名人は、無意識のなかでイメージを操作しているのです。 　暗記的算数の欠点はイメージをともなわないことにあるとわたしは考えています。 　そろばんを見て（イメージして）、明るい気持ちで、楽しくそろばんに取り組みましょう。 学院長　筒井保明