五玉の発明
前回、小学生低学年のみなさんを悩ませる「さくらんぼ計算」は、さまざまに考えられる計算の仕方のひとつだということを話しました。
基本として、数をドッツ（dot・dots）としてとらえられるなら、かんたんだよ、ともいいました。
数をドッツとしてとらえるというのは、
１は、●というドット。
２は、●●というドッツ。（英語は複数形になるとdotにsがついてdotsになります）
おなじように、
３は、●●●
４は、●●●●
５は、●●●●●
６は、●●●●●●
７は、●●●●●●●
８は、●●●●●●●●
９は、●●●●●●●●●
１０は、●●●●●●●●●●
１１は、●●●●●●●●●●＋●
１２は、●●●●●●●●●●＋●●
数字が大きくなるにつれ、●がどんどん増えていきます。もともとの数字のもとは、●に象徴されるなにかの物体です。●があらわすものは、🍎かもしれないし、🍊かもしれないし、🐶かもしれないし、🌳もしれません。１０００という数字をあらわすのに、数字がなかったら、●を１０００個、書かなければなりませんね。数字や算数は、計算の便利のために生まれたものです。
さくらんぼ計算というのは、８＋７の場合、●●●●●●●●＋●●●●●●●ということであり、ひとつずつ数えるのがめんどうなので、一けた、くりあがる１０（●●●●●●●●●●）をつくって、のこりの５（●●●●●）を足し、１５という答えを出すやり方です。さくらんぼ計算では、８（●●●●●●●●）＋７（●●●●●●●）を８（●●●●●●●●）＋２（●●）＋５（●●●●●）＝10＋5＝15と考えるので、なんだかめんどうに感じるのです。
でも、このやり方は、そろばんに似ていませんか？
もし、そろばんに五玉がなくて、一玉が９個だったら、さくらんぼ計算とおなじような考えかたをするのではないでしょうか。
でも、五玉がないそろばんは、幅が大きくなりますから持ち運びにも不便ですし、指を動かす回数もずいぶん増えてしまいます。
そこで、知恵のある誰かが、五玉を発明したわけです。
こんど、そろばんの練習をするとき、もし五玉がなかったら、と考えてみてください。五玉を考えた人は偉いなあ、と思うのではないでしょうか。
十進法を使用するわたしたちにとっては、現在のそろばんはとても効率的な形になっています。梁の上側に１つの五玉、梁の下側に４つの一玉という形です。
ところで、わたしが持っているそろばんは、梁の上側に２つの玉、梁の下側に５つの玉になっているものです。中国の尺貫法では1斤が16両と定められているので、16進法の計算ができるためだそうです。
また、コンピューターに使われる2進法の計算をするために、五玉だけの算盤もあるようです。
とてもおもしろいですね。
学院長 筒井保明
さくらんぼ計算は考えかたのひとつ
「さくらんぼ計算」は、考えかたのひとつであり、計算方法のひとつです。ところが、計算の答えがあっているにもかかわらず、やり方がさくらんぼ計算になっていないと、△や×をつけたり、ひどい場合は、叱ったりする小学校の先生がいるようです。
文科省としては、「こういう考え方もあるよ」というレベルの話なのですが、勘違いした先生が無理強いすると、子どもたちが混乱してしまいます。
小学校学習指導要領【算数編】から、小学生や保護者の方を悩ませるさくらんぼ計算に該当する部分を引用してみましょう。
「様々な計算の仕方が考えられる」と明記されています。
数字をドッツ（Dots）としてとらえられるなら、かんたんなことですし、わたしたちが頭のなかで無意識にやっていることでもありますから、さくらんぼ計算をめんどうに感じていやがる小学生の気持ちもわかりますね。
こういった問題は、そろばんにも、暗算にも、存在します。
江戸時代、そろばんには、多くの流派がありました。割り算にも九九があり、吉田松陰先生も松下村塾で教えていました。明治、大正、昭和の初めごろまで続いていたようですが、みなさんは、おぼえません。
現在では流派の色はあまり濃くないのですが、たとえば、かけ算のとき、かけられる数とかける数をそろばんに置くか置かないか、先生によって分かれたりします。両方置く先生、片方置く先生、どちらも置かない先生、また、生徒の学年や習熟度によって使い分ける先生がいます。
正しい答えを得ることにちがいはないのですから、どれを選ぶか、君たちが決めてもよいのです。
ところで、西洋式暗算Mental MathにもLeft to Right（左から右に計算する）派とRight to Left（右から左に計算する）派がいますが、わたしはLeft to Right（右から左に計算する）派です。つまり、大きい数のほうから計算します。
山手学院のそろばん指導者である西岡先生のような達人なら、ただちにそろばん式暗算で正確な答えを得るでしょうが、西洋式暗算の場合、たとえば、15,280円の品物と23,120円の品物を買うとき、15,000円と23,000円を先に足して38,000円を得てから、400円を得て38,400円になります。これが、西洋式暗算Left to Right（左から右に計算する）派の足し算です。「すばやく概算を得れば、生活上も便利ではないか」というのがLeft to Right（左から右に計算する）派です。
小学生低学年のみなさんは、もしかしたら、さくらんぼ計算に悩まされるかもしれませんが、計算の考えかた、計算のしかたは、いろいろあることを知ってください。
そろばんは、計算の考えかた、計算のしかたとして、歴史と伝統のあるものです。
リラックスして、たのしくそろばんに取り組みましょう。
学院長 筒井保明
そろばんが開く未来
渋沢栄一の『論語と算盤』の話を続けますと、渋沢のいう算盤は、「経済」という意味です。論語は、「道徳」という意味です。渋沢は、「論語と算盤を一致させる」という立場ですから、道徳の「徳」はそのまま「得」であり、経済は「徳＝得」の道だ、ということです。
経済は「徳＝得」の道、というようなことは解説書には書いてないかもしれませんが、渋沢栄一自身の本を読むかぎり、わたしはそう確信しています。
渋沢自身も「学者は誰も言わないけれど、論語を読むかぎり、孔子は理財に通じていたと、わたしは判断する」といっています。わたしも、渋沢の言葉から、「徳＝得」の道を歩んだのが渋沢の人生であったと考えます。
2021年の大河ドラマの主人公は渋沢栄一だそうですから、「徳＝得」の道、を念頭に置いて、ドラマを見るのもおもしろいでしょう。
さて、むずかしい理屈は抜きにして、渋沢栄一は、どんな少年だったでしょうか。
まず注目すべきなのは、たいへんな読書家であったこと。8歳から塾に通い、『論語』をはじめとして漢籍に親しみます。また、13歳のころ、道を歩きながら『絵本三国史』を読んでいて、溝の中に真っ逆さまに落ちました。
14歳になると、稼業の商売を始めました。紺屋（染め物屋）が染め物に使う藍玉などを商っていたようです。買い入れた藍を掛け売りしていましたから、掛け金の回収もあります。とうぜん、そろばんを弾きました。
17歳、奉行所から御用金400両の通達。このときの役人の態度に反骨心が沸き上がりました。
20歳、江戸末期の世相を見て、商人から武士になることを決意。
やがて渋沢栄一は、志士となり、縁あって一橋家に奉公し、四石二人扶持の武士となりました。
28歳、フランス・アメリカの視察に随行中、大政奉還が起こり、急遽、帰朝し、徳川家の財政を整理しました。
明治政府の建設とともに、太政官となり、大蔵省租税正に任ぜられ、明治４年、大蔵省に西洋式簿記を導入し、伝票によって金銭を出納しました。（伝票算は、全珠連の珠算検定では、3級以上の選択種目）
明治6年、自分の意見が採用されず、意見書を提出して、政府の職を辞しました。
これよりのち、あくまで民間の実業家として、活躍したのです。
かんたんに経歴をふりかえっても、論語と算盤が、渋沢栄一の根幹であることがわかりますね。
もし渋沢栄一に、論語だけで、算盤がなかったとしたら、商人になることも、徳川家の財政を整理することも、大蔵省租税正になることも、西洋式簿記を導入することも、銀行家になることも、なかったのではないでしょうか。
『論語』は渋沢栄一という人格をつくったといえます。おなじように、算盤は渋沢栄一の未来を開いたといえます。
渋沢栄一が生きている当時の評者は、「算盤を投じて剣をもった国士が、今度は剣を捨てて算盤を事とし、実業家たらんと志した」といいました。渋沢栄一ほど、褒められるばかりの大実業家はほかにはいないでしょう。
みなさんのそろばんは、みなさんの未来をどのように開くのでしょうか？
学院長 筒井保明
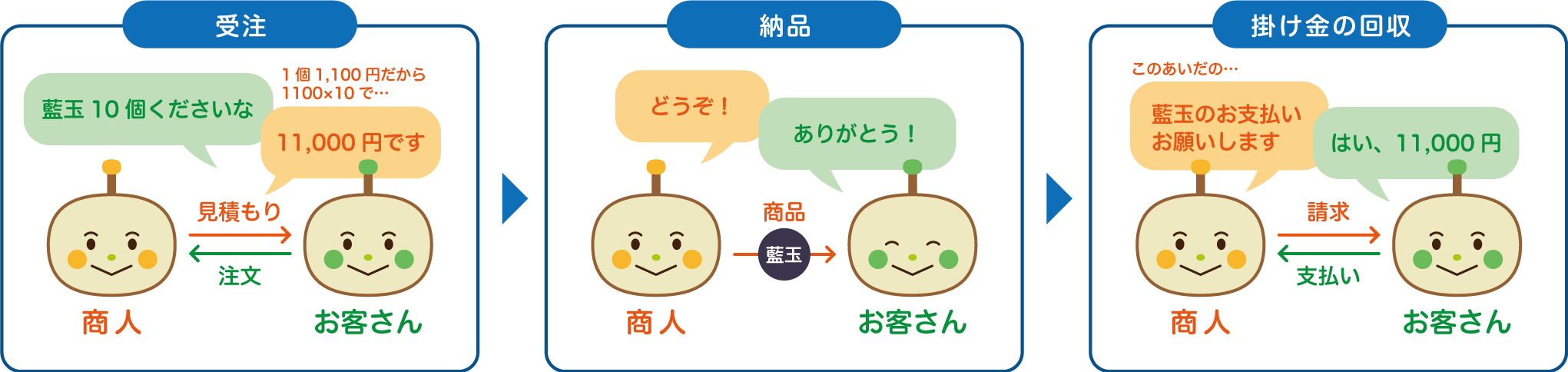
掛け売りとは？
注文を受けて商品を納品、後から代金が支払われる仕組み。江戸時代から現在まで利用されている文化です。
論語と算盤
9月に行われた自民党総裁選で、候補者の一人が「論語と算盤」という国家像を掲げました。埼玉県の偉人の一人である渋沢栄一の著書『論語と算盤』に想を得たものでしょう。
ずいぶんむかしの本ですが、渋沢栄一は2021年のＮＨＫ大河ドラマの主人公ですので、これからベストセラーとして復活するかもしれません。ただし、できれば、原文を読んでください。もともと口述筆記ですので、原文からは渋沢栄一の声が聞こえますが、現代語に書き直されたものからは聞こえません。
さて、『論語』は、中国の思想家である孔子の言行録です。渋沢栄一は、孔子の教えを人生の信条としていました。渋沢は、論語で一生を貫き、論語の精神で商売を続けました。「論語と算盤」は、いいかえれば、「道徳と経済」です。
『論語と算盤』のなかで、渋沢は「勉強」ということを強調します。しかし、わたしたちが使う意味では使っていません。訓読すれば「勉め強いる」ですから、「むりしてもやる」という意味であり、わたしたちは「勉強しなきゃ！」という感じで使っていますが・・・。
渋沢は、豊臣秀吉の長所中の長所が「勉強」であると主張します。
秀吉が織田信長の草履取りをしていたとき、冬であれば、信長の草履をふところに入れて温めていました。ここまで行き届くのは、よほどの「勉強」です。
信長が朝早く外出しようとするとき、秀吉はいつでも最初に信長の声に応じました。非凡な「勉強家」です。
本能寺の変のとき、岡山県から京都府まで、秀吉は軍を率いて13日で引き返しました。尋常ならざる「勉強家」であった証拠です。
渋沢は、秀吉のこの「勉強」が、秀吉に天下統一をなさしめたのだと断言します。
どうでしょうか。渋沢栄一の「勉強」のイメージがつかめたでしょうか。
『論語と算盤』を読んで感じてもらうしかないのですが、わたしたちのそろばんに置き換えていえば、「自分でそろばんを弾いて勉強しろ」というのが渋沢の言いたかったことです。「自分でそろばんを弾かないようなやつは立派になれないぞ」というアドバイスです。渋沢栄一は銀行家でもありましたから、小さな単位の計算違いも見逃しません。そろばんを弾くことを大切にしないようなやつに、大きなことを成功させることはできない、というのが彼の考えです。
明治４年、大蔵省に西洋式簿記を導入し、伝票によって金銭を出納することにしたのも渋沢栄一でした。伝票算は、全珠連の珠算検定では、3級以上の選択種目になっていますね。
現在の日本に必要なのは、渋沢栄一のような人物です。
残念ながら、自分でそろばんを弾いたことがないような人たちが、現在の日本を動かしています。
論語と算盤が一致していれば、また、道徳と経済が一体化していれば、日本は、現在のような事態にはなっていないはずです。
渋沢栄一の批判は、今日でも、そのまま続いています。そろばんを弾いている小学生のみなさんが大人になるころには、もっといい日本になっていることを願います。
「自分でそろばんを弾くこと」は、渋沢栄一のいう「勉強」のスタートです。
積極的に取り組みましょう。
学院長 筒井保明
山手学院朝霞台校がそろばんクラスを開講します！
山手学院のそろばんクラスは、全国珠算教育連盟の加盟校です。
全国珠算教育連盟は、1953年の9月に誕生した、珠算教育にたずさわる連盟です。1956年に社団法人、2013年に公益社団法人の認定を受け、責任ある珠算教育団体として、社会に資する役割が大きくなっています。
さて、山手学院がそろばんクラスをつくるきっかけになったのは、山手学院の数学教師たちにそろばん習得者が多いこと、計算の速さと正確さを兼ね備える生徒たちにそろばん学習者が多いことに気がついたからでした。
そろばんクラスの開講を考えたとき、最初に相談したのは、東京都知事認可の珠算学校の先生でした。ですから、もしかしたら山手学院そろばんクラスは、東京珠算教育連盟（“脳”活性化集団トーシュレン）でスタートしていたかもしれません。
ところが、山手学院の教師たちに段級位の確認をしますと、ほとんど全国珠算教育連盟の段級位であり、さらに日本商工会議所の珠算能力検定の級位でした。また、保護者の方々におたずねしても、やはり全国珠算教育連盟の段級位と日商の検定級位でした。
以上のようなことを話しますと、東京の珠算学校の先生は、
「そろばんの団体はたくさんあるから、いっそ山手連盟でもつくったら」 と冗談をいわれましたが、山手学院の生徒たちが段級位に挑戦していくなら、保護者の方々が持っている全国珠算教育連盟の段級位から始めよう、ということで、全国珠算教育連盟に加盟したのです。
埼玉県ということもあるのでしょうが、いまのところ、みなさんがお持ちの珠算資格は、全国珠算教育連盟と日商の段級位がほとんどです。ですから、全国珠算教育連盟でスタートしたことは正しかったと考えています。
そろばんの効用については山手学院そろばんクラスのパンフレットにまとめて書いていますので、ここでは触れませんが、珠算式暗算に力点を置いていることは強調してもいいでしょう。
そろばんという道具自体が、（触覚、聴覚も使いますが）視覚的なものですから、そろばんの習得は、筆算とはまったくちがう計算能力です。筆算は言語的操作（数字も抽象化された言語）ですが、そろばんは、そろばんという道具を使っていても、イメージ操作です。また、イメージ操作だからこそ、そろばんという道具が目の前になくても、珠算式暗算ができるようになるわけです。
前頭前野でイメージを操作することは、脳の重要な能力を培います。 もしかしたら、小学校教育として、そろばんが正式に導入されなかった原因は、言語学習中心の小学校教育になじまないと判断されたのかもしれません。小学３・４年生の教科書で、そろばんが紹介されるものの、文化史としてあつかわれている程度です。
昭和の初めごろから「そろばんはいつ始めるのがいいか」という議論がくりかえされますが、「そろばんは、できるだけ低学年から始めるべきだ」という意見にわたしは賛成です。
筆算で数字（抽象的な言葉）を操作する練習にくらべて、そろばんの球（具体的なもの）でイメージを操作する練習は、低学年の生徒ほど、なじみやすく、得意になることができるからです。
学院長 筒井保明
声を出して大きな数を数えよう！
1,000,000,000,000という数字を数えるとき、みなさんはどうやって数えますか？
一、十、百、千、万、十万、百万、千万、一億、十億、百億、千億、一兆と下から桁上がりに数えていって、1,000,000,000,000を「一兆」と答えるかもしれません。
最近の大企業には兆を超える売り上げの会社もありますから、わたしたちは大きな桁に慣れておく必要があります。
たとえば、住友電気工業株式会社の売上高は、3,107,027百万円です。
３兆１千７０億２千７百万円です。
アラビア数字では、3桁ごとにカンマを打ちます。
英語であれば、３桁ごとに読み方が変わりますので、カンマで区切られた数字を読むのはむずかしくありません。ところが、4桁ごとに読み方が変わる日本語では、カンマとズレますので、練習して読み慣れる必要があります。
１ one ワン 一
10 ten テン 十
100 one hundred ワン・ハンドレッド 百
1,000 one thousand ワン・サウザンド 千
ここまではいいのですが、
10,000 ten thousand テン・サウザンド 万
英語では、,000はサウザンドのままですが、日本語では0,000で「万」と読みます。
100,000 one hundred thousand ワン・ハンドレッド・サウザンド 十万
英語では、,00はハンドレッド、,000はサウザンドのままですが、日本語では、0,000が万ですから、100,000は十万と読みます。
1,000,000 one million ワン・ミリオン 百万
英語では、,000,000はミリオン。
1,000,000,000 one billion ワン・ビリオン 十億 日本語では、0が八個で億です。
1,000,000,000,000 one trillion ワン・トリリオン 一兆
3桁ごとに読み方が変わる英語と4桁ごとに読み方が変わる日本語ですが、3×４のトリリオンは、日本語でも４×３で「兆」と呼び名が変わりますので、おぼえやすいですね。
1,000,000,000,000,000 one quadrillion ワン・クアドリリオン 千兆
英語の場合、0が3個なら、サウザンド、０が6個なら、ミリオン、０が9個なら、ビリオンとおぼえていけばいいのです。
ところが、日本語の場合、10,000は0が4個だから一万、100,000,000は０が８個だから一億、とおぼえなければなりません。でも、大きな数字でも、声を出して何回も読む練習をしておけば、だいじょうぶです。
たとえば、36,985,247,856という数字があれば、数が八個の位置でのところが億ですから、369億8524万7856とすぐに数えられます。
そろばんが上達するほど、あつかう数が大きくなっていきます。
億、兆のような大きな数字は、声を出して読む練習をしておきましょう。
学院長 筒井保明
大学入試でかけ算の速さが役立つ！
小学生のみなさんにとって、大学入試はまだまだ先のことですが、そろばんや珠算式暗算に真剣に取り組んでおきますと、大学受験生になったとき、大きなアドバンテージを得ることができます。
山手学院高校部の生徒たちは、東大や京大をはじめとする国公立大学や私立難関大学を目指しています。化学の授業のとき、1⃣のような問題を解く場合、「時間が足りなかったら問４はあきらめるしかないだろう」という前提で、生徒たちに問題を解かせたところ、多くの生徒が時間切れになるなかで、3人の生徒が時間内にスッと終えたので、Ｓ先生は驚きました。
Ｓ先生の指導経験では、3ケタの数字のかけ算が入りますと、ほとんどの生徒の計算速度が落ち、時間切れになってしまうはずでした。
３人の生徒に「すごいなあ。どうしてそんなに速く計算できるんだ？」と聞きますと、
「珠算式暗算で計算しているんです」
３人ともおなじ返事でした。
みなさんも大学受験で化学を選択した場合には、1⃣のような問題を解くようになります。化学の計算の問題では、ともかく「かけ算が速いこと」が要求されます。かけ算でもたついていますと、あっという間に時間切れになり、合格点がとれなくなってしまいます。
ですから、かけ算が遅い生徒にとっては、時間がかかる計算問題はあきらめるしかありません。
ところが、珠算で鍛えられた3人にとっては、こんな計算問題など、お手のものです。Ｓ先生自身、計算は速いほうですが、この3人の速度には歯が立ちません。「そろばん、恐るべし」とＳ先生はいっています。ちなみに、問４の解き方は、つぎのようになります。
中学受験でも、高校受験でも、大学受験でも、計算を伴う入試問題に対する大きな課題は、計算速度です。なぜなら、入試には制限時間がありますから、計算が遅ければあきらかに不利になります。逆に、速くて正確な計算ができるならば、大きなアドバンテージになります。
この化学の問題を楽々と解く3人の高校生にとっては、むしろ計算で苦労している人たちのほうが不思議に見えるでしょう。計算は速ければ楽ですし、遅ければ苦痛です。
いま、そろばんや珠算式暗算に取り組んでいるみなさんは、ぜひ楽しく学習してください。算数も数学も計算が楽になれば、きっと楽しい教科になります。
学院長 筒井保明
そろばんで頭脳をきたえる！
日本で「右脳」という言葉を広めたのは、日本医科大学教授であった品川嘉也博士でしょう。ご本人は、交流があったことから、日本人として初めてノーベル物理学賞を受賞した湯川秀樹博士の最後の弟子と称していました。『意識と脳』（1982）ほか、多くの著作を読み直してみますと、大胆な、鋭い考察が多く、いまでもじゅうぶんに通用します。
現在では、すべての人に共通して右脳と左脳が分化しているわけではなく、「脳の機能のかたよりとして、左脳で言語をつかさどる人が多く、右脳でイメージをつかさどる人が多い」とします。また、女性よりも男性のほうが脳の分化がはっきりとしているようです。
そろばんが右脳を活性化するという主張の根拠も、じつは品川博士の実験に基づいています。
「右脳のイメージを使うことによって、脳の情報処理速度が飛躍的に上昇すること」を証明する実験に「そろばんの達人たち」が使われたのです。
数字や数学も一種の言語ですから、「九九は数を操作しているのではなく、言語操作にすぎない。つまり、九九の計算は、八十一個の熟語にすぎない」ということです。ですから、筆算は言語操作である、ということになります。計算は言語中枢を使いますので、左脳的ということです。
これに対して、品川博士は、脳波学的に、
「そろばんの達人たちは、計算しているときに言語中枢をほとんど使わず、右脳で計算している。頭のなかにそろばん球のイメージを浮かべて、イメージ操作をしながら右脳による計算をしている」
と主張します。これは珠算式暗算を習っているみなさんなら、当たり前の練習ですね。
品川博士の言葉を借りれば、そろばんの達人たちは、答えを「見ている」のです。
さて、そろばん熟達者のＡさんの脳波分析をおこなったところ、達人がかけ算見取り算の暗算をしているとき、ベータ２波（16.5–20Hz, 脳の思考活動の部位に強くあらわれる脳波）が右脳側と右後頭部（視覚野）に強く出ました。
また、達人のＢさんが、読み上げ算の暗算をおこなったところ、同様の結果になりました。読み上げ算にもかかわらず、聴覚野に相当する側頭部や言語中枢に強い脳波は出ませんでした。Ｂさんは、「計算中、ことばとして意識することはなく、言語は浮かんでこない。そろばんの球が浮かんで見える」といっています。この脳波の測定結果から、「そろばんは右脳を活性化する」といわれるようになりました。
たしかに、珠算式暗算はイメージ操作ですから、言語操作はしません。そして、イメージ操作は、言語操作よりも圧倒的に速いのです。
そろばんの達人たちだけでなく、アインシュタインなどに代表される物理学者たちや数学者たちも、イメージを操作して考える傾向が強いのです。数式で考えるわけではなく、イメージで考えて、数式で表現しているといってもいいかもしれません。
そろばんは、みなさんの頭脳をしっかりと鍛えます。
ぜひ楽しくそろばんの練習に取り組んでください。
学院長 筒井保明
学校が休みのあいだ、君がやるべきこと
新型コロナウイルスのために、世界中が混乱しています。とくにヨーロッパの国々は、歴史的にペストという疫病に苦しめられてきましたので、多くの人たちが強い恐怖を感じているでしょう。
緊急事態によって、学習の機会を失っている子どもたちが世界中にいます。
しかし、学校が休みだからといって、テレビやゲームやユーチューブの動画にたくさんの時間を費やしてしまうのは、自分の可能性の発展を止めてしまうことです。
なぜ、君たちにとって、テレビやゲームやユーチューブの動画は、よくないのでしょうか？
答えは、テレビやゲームやユーチューブの動画は、受け身でもじゅうぶんに楽しめてしまうメディアだからです。受け身で楽しめますから、あっというまに大量の時間が流れてしまいます。そして、受け身であるかぎり、君たちの思考力や創造力が鍛えられることはありません。
視覚・聴覚・嗅覚・触覚・味覚のうち、脳では視覚野がいちばん大きいので、テレビやゲームやユーチューブの動画は、わたしたちの脳をかんたんに独占することができます。いいかえれば、わたしたちは、自分の意志を使わずに、いつまでもラクラクと見続けることができます。
いっぽう、音だけのラジオ、文字だけの本、スクラッチなどは、受け身では楽しめないメディアです。ラジオであれば、自分の意志で音や声を聴かなければなりません。意識しないと、聞き逃して、話がわからなくなります。
本はもっとたいへんです。自分で意志をもって読まないかぎり、一ページも読むことはできません。受け身で本を読める人はいないはずです。
スクラッチもおなじです。自分で意志をもってプログラムしないかぎり、なにも始まりませんし、なにも動きません。ゲームは、誰かが組み立てたものをプレイすることですが、スクラッチは自分で組み立ててプレイするものです。自分で組み立てるためには、意志や思考が必要です。
スクラッチを開発したＭＩＴのミッチェル・レズニック博士は、ゲームでは育たない創造的思考力を培うためにスクラッチを推進しています。「ゲームに時間を使うなら、スクラッチをやろう！」ということです。
そろばんも、君たちが意志をもって使わないかぎり、そのままですね。そろばんが自分で計算するなんてことは、ありません。
じつは、小学生のみなさんの学力や能力を高めるものは、すべて自分でやらなければならないことばかりです。「読み・書き・そろばん」といいますが、読むことも、書くことも、そろばんの玉を弾くことも、自分の意志を必要としますね。すべて能動的な学習です。
学校が休みのあいだ、君たちがやるべきことは、この能動的な学習です。
小学生の学習の基本は音読ですから、毎日、音読してください。音読することによって、音読された言葉が自分の言葉になっていきます。そして、たくさん読書することです。
また、漢字を覚えたり、文章を書いたりしてください。さらに、絵をかいたり、工作したり、スクラッチしたりしてください。
もちろん、毎日、そろばんを練習してください。暗算に取り組んでいる小学生は暗算も練習してください。
能動的な学習によって、君たちの力はどんどん成長していきます。
学院長 筒井保明
珠算式暗算は脳の働きを高める！③
珠算式暗算の利点については、①②で書きました。
では、西洋の人たちは、どのように暗算をするのでしょうか？
西洋の人たちの暗算は、珠算式暗算にも応用できる部分もあり、数学的興味も尽きません。
アメリカで暗算といえば、知る人ぞ知るアーサー・ベンジャンミン博士（Arthur T. Benjamin, Ph.D.）です。『マス・マジック』という暗算の教材は、世界中で売れました。日本でも販売されましたので、保護者の方の中にも購入した方がいらっしゃるかもしれません。わたしもかつて購入した一人ですが、現在のベンジャミン博士の講義を視聴してみますと、ますます磨きがかかっています。その講義の内容をかいつまんでみましょう。
暗算は、英語でメンタル・マス（Mental Math）、メンタル・カルキュレーション（Mental calculation）といいます。
暗算の第一段階としては、左から右へ（left to right）で計算すること。たとえば、2300＋45であれば、自然に左から右へ、2345と計算するように、「左から右へ」がすべての計算において「より自然で速い」というのがベンジャミン博士の主張です。
暗算は、単純化のプロセスであり、たとえば、432×3は、3×400＝1200、3×30＝90、3×2＝6；1200＋90＋6＝1296と、最も大きい数から最も小さい数へと計算します。
54×7であれば、暗算の場合、7×50（350）と概算して、7×4（28）を足します。350＋28＝378となります。
ベンジャミン博士は、暗算や数字のおもしろさを伝えるために、さまざまな数字のマジックを紹介しながら、暗算の練習をうながします。
九九の9の段では、9×2＝18（1＋8＝9）、9×3＝27（2＋7＝9）、9×4＝36（3＋6＝9）、9×5＝45（4＋5＝9）、9×6＝54（5＋4＝9）、9×7＝63（6＋3＝9）、9×8＝72（7＋2＝9）、9×9＝81（8＋1＝9）で、9の段の答えの数字を足すと、みな9になります。
11のかけ算も数字のマジックで、2桁の数字に11をかけるときには、かけられる数字のまんなかにその数字の合計がはさまります。
たとえば、23×11 → 2＋3＝5 答えは253。同様に、35×11 → 3＋5＝8 答えは385。
41×11は？ 同じように考えれば、4＋1＝5ですから、451ですね。
ところで、48×11のように、4＋8＝12 足した数が二けたになった場合はどうしたらいいでしょうか？
4（12）8の場合は、（12）の1を繰り上げて、528とします。85×11なら、8（13）5ですから、935です。
では、3桁の数字に11をかける場合はどうでしょうか？
たとえば、314×11 → (3＋1＝4)（1＋4＝5）→ 314のまんなかの数字に置き換えて3（4）（5）4、答えは3454となります。425×11を同じようにやってみてください。暗算でできましたか？ 4675ですね。
ベンジャミン博士は、アメリカ人ですので、00をハンドレッドhundredと読み、たとえば1100という数字は、イレブン・ハンドレッド、3300という数字はサーティ・スリー・ハンドレッドと表現します。わたしは、最初、とまどいました。
ともあれ、メンタル・マス（暗算）は、左から右へ（Left to Right）です。
学院長 筒井保明